You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
Example 1:

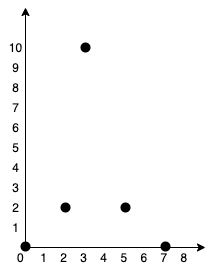
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation:
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.

Example 2:
Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18
Constraints:
1 <= points.length <= 1000$-10^6$ <= xi, yi <= $10^6$(xi, yi) are distinct.給定一個整數矩陣 points, 其中每個 entry points[i] = [$x_i, y_i]$ 代表 2 維平面上的座標點
定義平面上認兩點 points[i], points[j] 的 manhattan dist 為 $|x_i - x_j| + |y_i - y_j|$
要求寫一個演算法算出要連接所有座標點